6 класс
Математика
Задача 1. Дано уравнение 13х+10у=2017, где х и у – натуральные числа. Найдите наименьшее возможное значение у в данном уравнении (в ответе указываете только число)
Автор: заведующий кафедрой физико-математического образования ИРОиПК, кандидат педагогических наук Баишева М.И.
Задача 2. Какое наибольшее количество последовательных натуральных чисел можно записать, чтобы сумма цифр каждого из этих чисел не делилась на 5?
Автор: лауреат государственной премии М.А. Алексеева, Заслуженный Учитель РС(Я) Кысылбаиков И.Г.
Задача 3. Сколько произведений, кратных десяти, можно образовать из чисел 2, 3, 5, 5, 7, 9?
Автор: заведующий кафедрой методики преподавания математики ИМИ СВФУ, кандидат педагогических наук Ефремов В.П.
Задача 4. Вася написал на доске четырехзначное число. Петя заметил, что третья цифра этого числа втрое больше чем первая цифра и втрое меньше чем вторая цифра. Какое число написал Вася, если известно, что это число нацело делится на 13?
Автор: старший преподаватель кафедры “Математический анализ” ИМИ СВФУ, призер всероссийских и международных олимпиад по математике Марков В.Г.
Задача 5. 13 ноября 2017 года день рождения Первого президента Республики Саха (Якутия) Михаила Ефимовича Николаева. Возраст, который исполнится ему в этом году, записан в виде выражения 2017 – 1937. Вычеркните четыре различные цифры, так чтобы получилось наименьшее натуральное число. При этом из каждого числа надо вычеркнуть хотя бы по одной цифре. В ответе укажите полученное наименьшее натуральное число.
Автор: учитель математики МБНОУ «Октемский НОЦ», отличник образования РС(Я), победитель республиканского конкурса «Учитель года РС(Я)» Егоров А.А.
Информатика
Задача 1. Банкир Богатеев, набирая код на своем сейфе, каждую кнопку циферблата нажал то количество раз, какое значение написано на ней. Циферблат сейфа содержит все цифры от 1 до 9. Сколько раз Богатеев нажимал на кнопки?
Автор: учитель информатики «Октемского лицея» с УИОП МБНОУ «Октемский НОЦ» Ковров Ф.Ф.
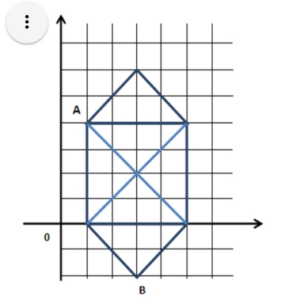
Задача 2. Красная Шапочка испекла пирожков и собралась идти в гости к бабушке, которая живет в лесу. Чтобы не попасть Волку, ей надо пройти маршрут в лесу (см. рис. ниже), не проходя дважды по одной и той же линии. Ей в этом помог Охотник. Он с помощью Исполнителя Чертежник составил соответствующий алгоритм пути Красной Шапочки из дома (А)через дом Бабушки (В) обратно домой (А). Исполнитель Чертежник перемещается на координатной плоскости, оставляя след в виде линии. Чертежник может выполнять команду: Сместиться на (a, b),перемещающую его из точки с координатами (x, y) в точку с координатами(x+a, y+b). Вначале Чертежник находится в точке А с координатами (1, 4).К сожалению, листочек попал под дождь и некоторые числа исчезли. Надо определить эти числа и ответить на вопрос, сколько раз повторяется команда Сместиться на (-2, -2)в алгоритме, чтобы выполнялось условие задачи:
Сместиться на (4, 0)
Сместиться на (-2, 2)
Сместиться на (…, …)
Сместиться на (4, -4)
Сместиться на (0, 4)
Сместиться на (…, …)
Сместиться на (4, 0)
Сместиться на (…, …)
Сместиться на (…, …)
Сместиться на (0, 4)
Автор: доцент кафедры теории и методики обучения информатики Института математики и информатики СВФУ Винокурова Е.С.
Задача 3. Некоторое число из таблицы (см. рис. ниже) закодировано последовательностью цифр: 1102. Определите это число.
| 27 | 9 | 3 | 1 |
| 28 | 10 | 4 | 2 |
| 29 | 11 | 5 | 2 |
| 30 | 12 | 6 | 4 |
| 31 | 13 | 6 | 5 |
| 32 | 14 | 7 | 5 |
| 33 | 15 | 7 | 7 |
| 34 | 16 | 8 | 8 |
| 35 | 17 | 8 | 8 |
| 36 | 18 | 12 | 10 |
| 37 | 18 | 13 | 11 |
| 38 | 19 | 14 | 11 |
| 39 | 19 | 15 | 13 |
| 40 | 20 | 15 | 14 |
| 41 | 20 | 16 | 14 |
| 42 | 21 | 16 | 16 |
| 43 | 21 | 17 | 17 |
| 44 | 22 | 17 | 17 |
| 45 | 22 | 21 | 19 |
| 46 | 23 | 22 | 20 |
| 47 | 23 | 23 | 20 |
| 48 | 24 | 24 | 22 |
| 49 | 24 | 24 | 23 |
| 50 | 25 | 25 | 23 |
| 51 | 25 | 25 | 25 |
| 52 | 26 | 26 | 26 |
| 53 | 26 | 26 | 26 |
| 54 | 36 | 30 | 28 |
| 54 | 37 | 31 | 29 |
| 55 | 38 | 32 | 29 |
| 55 | 39 | 33 | 31 |
| 56 | 40 | 33 | 32 |
| 56 | 41 | 34 | 32 |
| 57 | 42 | 34 | 34 |
| 57 | 43 | 35 | 35 |
| 58 | 44 | 35 | 35 |
| 58 | 45 | 39 | 37 |
| 59 | 45 | 40 | 38 |
| 59 | 46 | 41 | 38 |
| 60 | 46 | 42 | 40 |
| 60 | 47 | 42 | 41 |
Автор: студент 4-го курса Б-ИНФ-14 Института математики и информатики СВФУ Попов С.А.
Физика
Задача 1. Два автомобиля движутся по прямому участку автострады с постоянными скоростями 54 км/ч и 36 км/ч. Сначала расстояние между автомобилями было равно 1 км. Сколько км проедет второй автомобиль, когда его догонит первый автомобиль? Ответ напишите в км.
Автор: учитель физики МБНОУ «Октемский НОЦ», кандидат педагогических наук, лауреат государственной премии им. М.А. Алексеева победитель республиканского конкурса «Учитель года РС(Я)» Семенов А.А.
Задача 2. Деревянный брусок имеет массу 10 кг. Какой станет масса бруска, если одну из его сторон уменьшить в 5 раз, а два других увеличить в два раза каждый? Ответ напишите в граммах.
Автор: учитель физики МБНОУ «Октемский НОЦ», кандидат педагогических наук, лауреат государственной премии им. М.А. Алексеева победитель республиканского конкурса «Учитель года РС(Я)» Семенов А.А.
Задача 3. Ближайшее сближение планет Земля и Марс было зафиксировано в 2003 году, когда они находились только в 34,8 млн. миль друг от друга. Самое большое расстояние между планетами (250 миллионов миль друг от друга) будет, когда Земля и Марс находятся на противоположных сторонах от Солнца. На сколько минут будет опаздывать радиосигнал, посланный в этот момент из Земли и пойманный обратно, от сигнала, посланного и пойманного в момент наибольшего сближения? (Скорость радиосигнала равна 299 800 км в секунду, одна миля примерно равна 1600 метров.). Ответ напишите в мин.
Автор: учитель физики МБНОУ «Октемский НОЦ», кандидат педагогических наук, лауреат государственной премии им. М.А. Алексеева победитель республиканского конкурса «Учитель года РС(Я)» Семенов А.А.
7 класс
Математика
Задача 1. Дано уравнение 13х-10у=2017, где х и у – натуральные числа. Найдите наименьшее возможное значение х в данном уравнении.
Автор: заведующий кафедрой физико-математического образования ИРОиПК, кандидат педагогических наук Баишева М.И.
Задача 2. Дано число 1836549. В одном ходе можно брать две соседние ненулевые цифры и менять их местами, после чего вычесть из каждой из них по 1. Какое наименьшее число может получиться после некоторого количества таких ходов?
Автор: лауреат государственной премии М.А. Алексеева, Заслуженный Учитель РС(Я) Кысылбаиков И.Г.
Задача 3. Выпишите в порядке возрастания последовательность целых чисел, удовлетворяющих неравенству (в ответе укажите восьмидесятое число этой последовательности):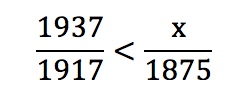
Автор: учитель математики МОБУ СОШ №12 ГО «Город Якутск», заслуженный учитель Республики Саха (Якутия), Почетный работник общего образования Российской Федерации Чиряев А.К.
Задача 4. Отцу – 41 год, старшему сыну – 13 лет, дочери – 10 лет, а младшему сыну – 6 лет. Через сколько лет возраст отца окажется равным сумме лет его детей?
Автор: заведующий кафедрой методики преподавания математики ИМИ СВФУ, кандидат педагогических наук Ефремов В.П.
Задача 5. Какое наибольшее число фишек можно расставить на шахматной доске так, чтобы каждая клетка, на которой стоит фишка, имела общую сторону ровно с тремя клетками, на которых не стоят фишки.
Автор: заведующий кафедрой “Математический анализ” ИМИ СВФУ, доктор физико-математических наук, профессор Попов С.В.
Задача 6. В этом году республика отмечает 80-летие Первого Президента РС(Я) Михаила Ефимовича Николаева. Какое число стоит в последовательности 1.2.2.3.3.3.4.4.4.4.5.5.5.5.5…. на 80 месте?
Автор: учитель математики МБНОУ «Октемский НОЦ», почетный работник РФ, отличник образования РС(Я) Гермогенова В.Н.
Информатика
Задача 1. Винтик поставил на скачивание файл и определил, что закачка займет 20 минут. Через 4 минуты на этом же компьютере Шпунтик поставил на скачивание свой файл. После того как файлы были скачаны, выяснилось, что объем файла Шпунтика на 20% больше файла Винтика. При скачивании двух файлов скорость скачивания каждого в два раза ниже первоначальной, при скачивании одного – равна первоначальной. С какой разницей в минутах закончилось скачивание файлов?
Автор: учитель информатики «Октемского лицея» с УИОП МБНОУ «Октемский НОЦ» Ковров Ф.Ф.
Задача 2. Шерлоку Холмсу попала записка от некоего человека N. Записка была в зашифрованном виде: UAUEEYTOIUSEYDTRTPODHETIUNTHFLEUDSWFFВ процессе шифровки и дешифровки используется цифровой ключ – слово с неповторяющимися знаками. Дешифрование можно сделать, зная этот ключ. Шерлок Холмс выяснил, что цифровой ключ к данному сообщению – 3417256, и что для этой записки был использован следующий алгоритм шифровки:1. Подсчитать количество знаков в исходном шифруемом тексте.2. Разделить это число на количество знаков цифрового ключа и выбрать ближайшее целое число, которое больше или равно полученному числу. Например, если в сообщении 42 символа, а число знаков ключа равно 5, то 42:5 =8 (остаток 2). Поэтому выбирается число 9.3. Построить таблицу так, что количество столбцов равно количеству знаков ключа, а число строк равно числу, выбранному в п.2. 4. Над таблицей записать цифровой ключ (знаки ключа в той же последовательности, в которой они заданы).5. Заполнить строки слева направо символами сообщения, начиная с верхней строки. Для указанного примера в каждом столбце будет по 8 символов, а в двух первых слева столбцах – по 9.6. В порядке возрастания знаков ключа по столбцам таблицы (вертикально, сверху вниз) прочитать и выписать зашифрованный текст. Зная алгоритм шифровки, помогите Шерлоку Холмсу расшифровать данное сообщение. При вводе ответа расшифрованное сообщение записать без пробелов заглавными буквами.
Автор: доцент кафедры теории и методики обучения информатики Института математики и информатики СВФУ Винокурова Е.С.
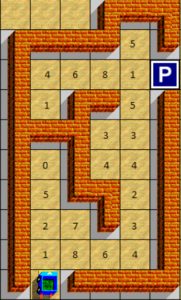
Задача 3. Исполнитель Тележка должен добраться до Портала (см. рис), выполнив команды приведенного ниже алгоритма. Определите значение переменной X, используя следующую справочную информацию:
« { » – начало блока алгоритма;
« } » – конец блока алгоритма;
«портал» обозначен в лабиринте значком с буквой «P»;
команда «вперед» передвигает тележку на одну клетку вперед;
команда «налево» разворачивает тележку на 90 градусов влево;
команда «направо» разворачивает тележку на 90 градусов вправо;
команда «увеличить X на» увеличивает текущее значение X на значение клетки;
команда «уменьшить X на» уменьшает текущее значение X на значение клетки;
«портал» имеет значение 0.
{
X = 0;
вперед;
пока ( не портал )
{
если ( слева_свободно )
{
налево;
вперед;
уменьшить X на ( значение_клетки );
}
иначе
если ( впереди_свободно )
{
вперед;
увеличить X на ( значение_клетки );
}
иначе
{
направо;
уменьшить Х на ( значение_клетки );
}
}
}
Автор: студент 4-го курса Б-ИНФ-14 Института математики и информатики СВФУ Попов С.А.
Физика
Задача 1. Два автомобиля движутся по прямому участку автострады с постоянными скоростями 54 км/ч и 36 км/ч. Сначала расстояние между автомобилями было равно 1 км. Найти максимальное время, когда расстояние между автомобилями станет равным 200 м? Ответ напишите в сек.
Автор: учитель физики МБНОУ «Октемский НОЦ», кандидат педагогических наук, лауреат государственной премии им. М.А. Алексеева победитель республиканского конкурса «Учитель года РС(Я)» Семенов А.А.
Задача 2. Эйфелева башня имеет высоту 300 м и массу 7200 т. Какой массы окажется макет этой башни высотой 1,5 м, сделанный из материала по плотности в три раза меньшей, чем материал башни? Ответ напишите в гр.
Автор: учитель физики МБНОУ «Октемский НОЦ», кандидат педагогических наук, лауреат государственной премии им. М.А. Алексеева победитель республиканского конкурса «Учитель года РС(Я)» Семенов А.А.
Задача 3. При очистке реки от разлива нефти собрали 100 м3 загрязненной жидкости. Ее средняя плотность оказалась равной 900 кг/м3. Сколько тонн нефти удалось собрать, если плотность нефти равна 800 кг/м3, а плотность воды равна 1000 кг/м3? Ответ напишите в тоннах.
Автор: учитель физики МБНОУ «Октемский НОЦ», кандидат педагогических наук, лауреат государственной премии им. М.А. Алексеева победитель республиканского конкурса «Учитель года РС(Я)» Семенов А.А.